Fractal Gh
Mandelbrot Fractal Generator
Section titled “Mandelbrot Fractal Generator”JavaScript app that draws the Mandelbrot fractal and allows you to zoom in and explore the fractal (uses zero libraries). Launches in fullscreen mode for maximum impact on desktop, and has a responsive mobile compatible design with a multi-touch interface on mobile devices.
Fractals Album


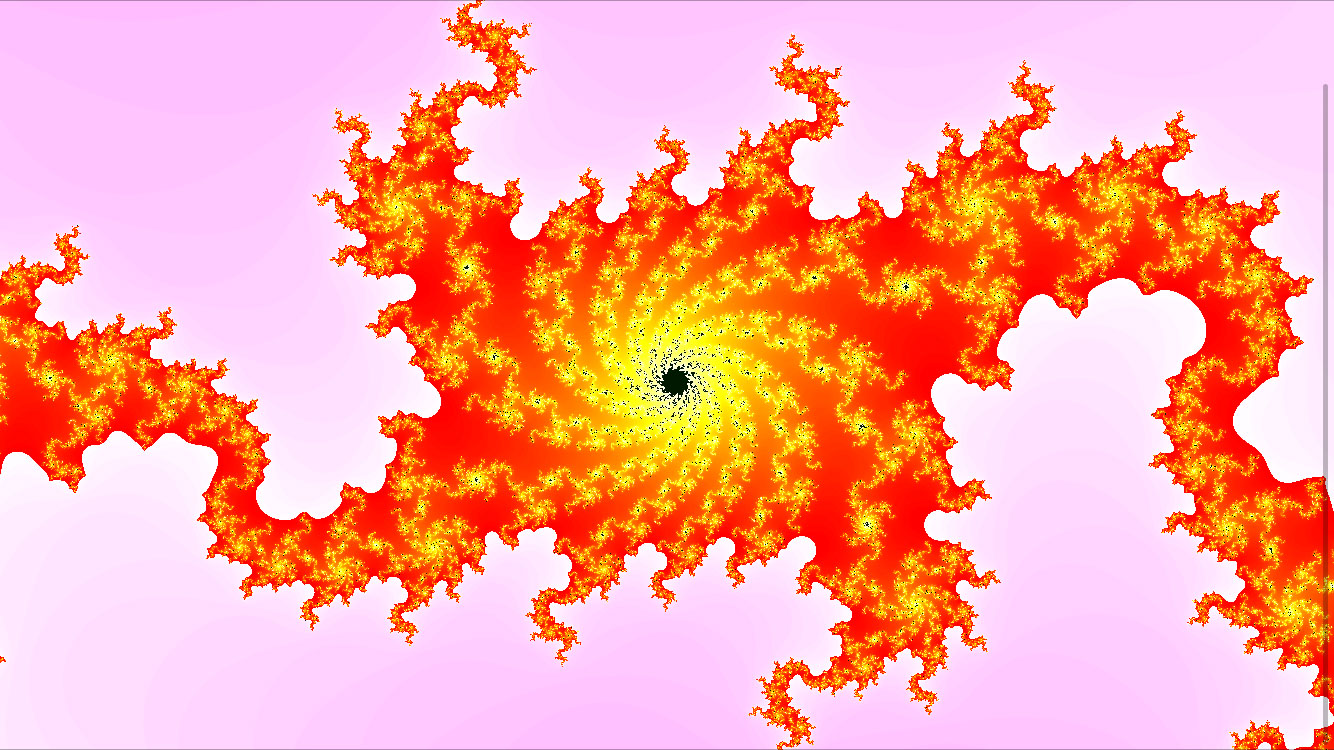






The coloring algorithm adjusts to the number of colors needed (i.e. the maximum escape time for the Mandelbrot set generation). See below for more info on the coloring algorithm.
Fractal API
Section titled “Fractal API”fractal.js is designed to work independently from app.js and can easily be integrated into any project. It provides an api through its update function, which takes an options object that instructs the fractal how to adjust itself before it re-renders.
// create fractal object, send it an HTML canvas element// on which it will draw itselfvar fractal = new Fractal(fractalCanvasElement);
// tell the fractal to update itself based on the options sent// it will only redraw itself if necessaryfractal.update(options);// fractal api as an options object// all keys are optionalvar options = {
// set size of canvas // set pixel width of canvas pxWidth: number, // e.g. 2880
// set pixel height of canvas pxHeight: number, // e.g. 1800
// reset to default settings (coordinates, max escape time, and // starting options - does not reset canvas size) defaults: true,
// reset to default cartesian coordinates (shows the whole fractal) resetToDefaultCords: true,
// draw the fractal at these specific cartesian coordinates cords: { xCartMin: number, // e.g. -2.1 xCartMax: number, // e.g. 0.8, yCartMin: number, // e.g. -1.2, yCartMax: number // e.g. 1.2 },
// set the maximum escape time // numbers < 14 will be converted to 14 // numbers > 1792 will be converted to 1792 maxEscapeTime: number, // e.g. 224
// pixel coordinates on canvas of point to zoom in on zoomInPxPoint: { xPx: number, // e.g. 100 yPx: number // e.g. 100 },
// pixel coordinates on canvas of point to zoom out from zoomOutPxPoint: { xPx: number, // e.g. 100 yPx: number // e.g. 100 },
// pixel coordinates of rectangle on canvas to zoom in on zoomInPxBox: { xPxMin: number, // e.g. 50 xPxMax: number, // e.g. 100 yPxMin: number, // e.g. 50 yPxMax: number // e.g. 100 },
// set the current options as the starting options // the fractal resets to its starting options when told to reset setAsStartingOptions: bool, // e.g. true
// reset cartesian coordinates to starting cartesian coordinates resetCords: bool, // e.g. true
// reset the max escape time to the starting max escape time resetMaxEscapeTime: bool, // e.g. true
// draw with distortion if the ratio of canvas width/height doesn't // match the ratio of cartesian coordinates width/height // by default (if this is omitted or false) the cartesian coordinates are // adjusted to match the ratio of the canvas width/height to avoid distortion distortion: bool // e.g. true}Coloring Algorithm
Section titled “Coloring Algorithm”The seven case are:
case 0: R=0, B=0, increase green from 0 to 255
case 1: R=0 G=255, increase blue from 0 to 255
case 2: G=255, B=255, increase red form 0 to 255
case 3: G=0, B=255, increase red from 0 to 255
case 4: R=255, B=255, increase green from 0 to 255
case 5: R=255, B=0, increase green from 0 to 255
case 6: R=255, G=255, increase blue from 0 to 255
Fractal.prototype.rgbNum = function(escapeTime){ if (escapeTime <= 2) { //pin all escape times less than 3 to black return [0, 0, 0]; } else if (escapeTime === this.maxEscapeTime) { //normally this would be white, but that's too much white, so override return [0, 25, 0]; }
var redNum; var greenNum; var blueNum; var rgbIncrements = Math.floor(((this.maxEscapeTime) / 7)); var caseNum = Math.floor(escapeTime / rgbIncrements); var remainNum = escapeTime % rgbIncrements;
switch (caseNum) { case 0: redNum = 0; greenNum = Math.floor(256 / rgbIncrements) * remainNum; blueNum = 0; break; case 1: redNum = 0; greenNum = 255; blueNum = Math.floor(256 / rgbIncrements) * remainNum; break; case 2: redNum = Math.floor(256 / rgbIncrements) * remainNum; greenNum = 255; blueNum = 255; break; case 3: redNum = Math.floor(256 / rgbIncrements) * remainNum; greenNum = 0; blueNum = 255; break; case 4: redNum = 255; greenNum = Math.floor(256 / rgbIncrements) * remainNum; blueNum = 255; break; case 5: redNum = 255; greenNum = Math.floor(256 / rgbIncrements) * remainNum; blueNum = 0; break; case 6: redNum = 255; greenNum = 255; blueNum = Math.floor(256 / rgbIncrements) * remainNum; break; }
return [redNum, greenNum, blueNum];};