Quine-McCluskey Algorithm

Unique Algorithms

Quine-McCluskey Algorithm

A comprehensive Python implementation of the Quine-McCluskey algorithm for Boolean function minimization. This algorithm systematically finds prime implicants, essential prime implicants, and generates all minimum sum of products forms for Boolean functions with up to 26 variables.

Algorithm Execution Examples

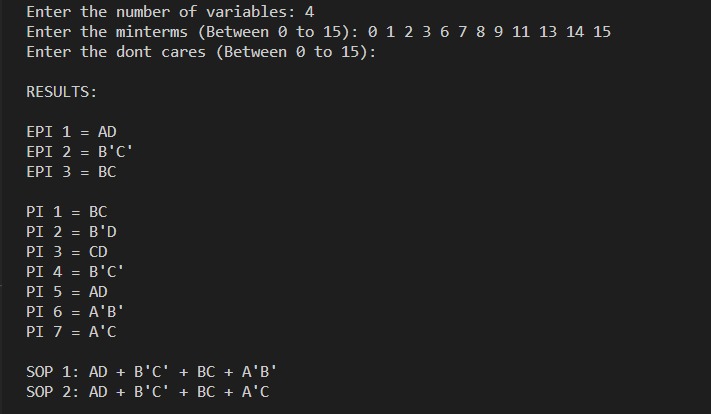
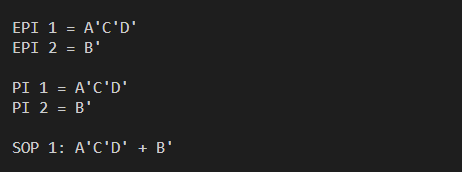
Theoretical Foundation

The Quine-McCluskey algorithm is a tabular method for minimizing Boolean functions. It provides an exact solution for finding the minimal sum of products (MSOP) representation, making it fundamental to digital logic design and optimization.

Mathematical Background

Given a Boolean function $f: \{0,1\}^n \rightarrow \{0,1\}$, the algorithm finds the minimal expression:

$$f_{min} = \sum_{i=1}^{k} P_i$$

Where each $P_i$ is a prime implicant and the sum represents logical OR operation.

Algorithm Phases

The algorithm operates in two main phases: finding prime implicants and selecting essential ones for minimal coverage.

Phase 1: Prime Implicant Generation

1. List Minterms: Enumerate all minterms where function evaluates to 1
2. Group by Ones: Group minterms by number of 1s in binary representation
3. Combine Terms: Iteratively combine terms that differ by exactly one bit
4. Mark Combined: Remove terms that were successfully combined
5. Repeat: Continue until no more combinations possible
6. Extract Primes: Unmarked terms are prime implicants

Phase 2: Prime Implicant Selection

1. Coverage Table: Create table showing which prime implicants cover which minterms
2. Essential Primes: Identify prime implicants that uniquely cover minterms
3. Select Essential: Include all essential prime implicants in final expression
4. Cover Remaining: Select minimal subset of remaining primes for complete coverage
5. Generate Solutions: Produce all minimal sum of products forms

Implementation Features

The implementation provides both interactive and programmatic interfaces with comprehensive output analysis.

Supported Operations

• Prime Implicant Discovery: Systematic finding of all prime implicants
• Essential Prime Identification: Automatic detection of essential prime implicants
• Multiple Solutions: Generation of all minimum sum of products forms
• Don’t Care Handling: Support for don’t care conditions in specification
• Variable Limitation: Support for up to 26 variables (A-Z)

Usage Modes

Interactive Mode

python main.py

Provides step-by-step guided input with real-time visualization of the minimization process.

Batch Mode

python main.py <variables> <minterms> -d <dont_cares>

Example with don’t cares:

python main.py 4 0 1 2 3 4 -d 5 6 7 8

Example without don’t cares:

python main.py 3 0 4 2 6 7

Algorithm Complexity

The computational complexity grows exponentially with the number of variables, making it suitable for moderate-sized problems.

Time Complexity Analysis

• Minterm Generation: $O(2^n)$ for n variables
• Combination Phase: $O(m^2 \cdot n)$ where m is number of minterms
• Coverage Analysis: $O(p \cdot m)$ where p is number of prime implicants
• Solution Generation: Exponential in worst case for multiple minimal solutions

Space Complexity

• Storage Requirements: $O(2^n)$ for complete truth table representation
• Intermediate Terms: $O(m \cdot n)$ during combination phase
• Result Storage: $O(p)$ for prime implicants and minimal solutions

Applications

The Quine-McCluskey algorithm is fundamental to:

• Digital Logic Design: Minimization of combinational logic circuits
• Computer Architecture: Optimization of arithmetic and logic units
• VLSI Design: Reduction of transistor count in integrated circuits
• Formal Verification: Analysis of Boolean specifications
• Educational Tools: Teaching of logic minimization concepts

Comparison with Other Methods

The Quine-McCluskey algorithm offers distinct advantages compared to alternative minimization techniques.

vs. Karnaugh Maps

Quine-McCluskey Advantages:

• Scalability: Works with more than 6 variables systematically
• Algorithmic: Suitable for computer implementation
• Completeness: Guaranteed to find minimal solutions
• Multiple Solutions: Finds all minimal expressions

Karnaugh Map Advantages:

• Visual Intuition: Easier for small numbers of variables
• Manual Speed: Faster for 2-4 variable problems
• Pattern Recognition: Human-friendly for simple cases

vs. Espresso Algorithm

Quine-McCluskey:

• Exact Method: Guaranteed minimal results
• Educational Value: Clear theoretical foundation
• Systematic: Well-defined algorithmic steps

Espresso:

• Heuristic: Faster for large problems
• Practical: Better for real-world circuit sizes
• Optimization: Additional heuristic improvements

Implementation Details

The Python implementation uses efficient data structures and algorithms:

• Bit Manipulation: Fast binary operations for term combination
• Set Operations: Efficient coverage analysis
• Recursive Search: Exhaustive solution enumeration
• Memory Optimization: Minimal intermediate storage

Usage Examples

The algorithm handles various Boolean function specifications effectively.

Example: 4-Variable Function

Input specification for function with minterms (0,1,2,3,4) and don’t cares (5,6,7,8):

python main.py 4 0 1 2 3 4 -d 5 6 7 8

Output provides:

• Prime implicants with binary representations
• Essential prime implicants identification
• All minimal sum of products forms
• Coverage analysis tables

Example: 3-Variable Function

Simple function without don’t cares:

python main.py 3 0 4 2 6 7

Demonstrates algorithm operation on smaller problem spaces with clear visualization of each step.

Limitations and Extensions

Current Limitations:

• Variable Count: Maximum 26 variables due to naming convention
• Exponential Growth: Becomes impractical for very large functions
• Memory Usage: Truth table storage for large variable counts

Potential Extensions:

• Heuristic Pruning: Early elimination of non-essential terms
• Parallel Processing: Distributed computation for large problems
• Incremental Updates: Efficient modification of existing solutions
• Output Formats: Support for VHDL, Verilog, and other HDLs

Implementation Notes

This implementation serves as both an educational tool and a practical utility for digital logic design, providing clear visualization of algorithmic steps and comprehensive analysis of Boolean function minimization.